Chapter 2 Basics of SIMD Programming
While Chapter 1 is designed to provide a general idea of Cell programming, Chapter 2 is intended as an introduction for programmers to the use of SIMD technology, one of the characteristic features of Cell programming.
Capable of processing multiple data with a single instruction, SIMD operations are widely used for 3D graphics and audio/video processing in multimedia applications. A number of recently developed processors have instructions for SIMD operations (hereinafter referred to as SIMD instructions). In multimedia extensions for the Intel x86, for example, SSE instructions and MMX instructions are defined as SIMD instructions. The Cell described in this tutorial includes two types of SIMD instructions – VMX instructions implemented in the PPE and SPU SIMD instructions implemented in SPEs.
In this chapter, SIMD programming is explained using the VMX instructions implemented in the PPE. We will look at what SIMD programming is, what data it uses and how it is performed. A number of sample programs are presented to make it easier to acquire necessary programming skills. Review questions are also provided at the end of the chapter.
SIMD programming on SPEs is covered in Chapter 3.
Table 2.1: Structure of Chapter 2
|
Section |
Title |
Description |
|
Section 2.1 |
SIMD Operation Overview |
Explains the fundamentals of SIMD operations. |
|
Section 2.2 |
Data Used in SIMD Programming |
Provides a general rundown on the data and data types used in SIMD programming. |
|
Section 2.3 |
Rudimentary SIMD Operations |
Demonstrates basic SIMD operations. |
|
Section 2.4 |
Generation of SIMD-Ready Vectors |
Describes how to organize data to make it fit SIMD operations. |
|
Section 2.5 |
Elimination of Conditional Branches |
Describes how SIMD operations eliminate the use of conditional branches. |
|
Section 2.6 |
Exercise (2-1): Total Calculation Program |
Provides a review question that can be solved based on what we will learn in Section 2.3. |
|
Section 2.7 |
Exercise (2-2): Floating-Point Calculation Program |
Provides a review question that can be solved based on what we will learn in Section 2.4. |
|
Section 2.8 |
Exercise (2-3): Absolute Value Calculation Program |
Provides a review question that can be solved based on what we will learn in Section 2.5. |
|
Section 2.9 |
Exercise (2-4): Grayscale Conversion Program |
As a comprehensive review of Chapter 2, provides a review question about color to grayscale conversion. |
2.1 SIMD Operation Overview
Let’s start with the unique aspects of SIMD operations. SIMD is primarily geared towards graphics applications and physics calculations that require simple, repetitive calculations of enormous amounts of data.
2.1.1 How SIMD Operates
SIMD is short for Single Instruction/Multiple Data, while the term SIMD operations refers to a computing method that enables processing of multiple data with a single instruction. In contrast, the conventional sequential approach using one instruction to process each individual data is called scalar operations.
Using a simple summation as an example, the difference between the scalar and SIMD operations is illustrated below. See Fig. 2.1 for how each method handles the same four sets of additions.
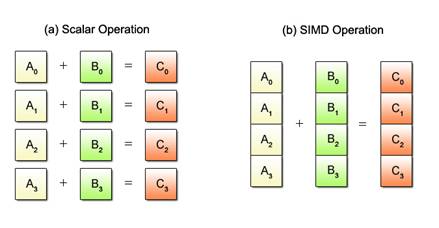
Fig. 2.1: Scalar vs. SIMD Operations
With conventional scalar operations, four add instructions must be executed one after another to obtain the sums as shown in Fig. 2.1 (a). Meanwhile, SIMD uses only one add instruction to achieve the same result, as shown in Fig. 2.1 (b). Requiring fewer instructions to process a given mass of data, SIMD operations yield higher efficiency than scalar operations.
2.1.2 Restrictions on SIMD Operations
Despite the advantage of being able to process multiple data per instruction, SIMD operations can only be applied to certain predefined processing patterns. Fig. 2.2 shows one such pattern where the same add operation is performed for all data.
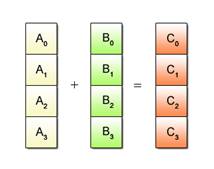
Fig. 2.2: Example of SIMD Processable Patterns
SIMD operations cannot be used to process multiple data in different ways. A typical example is given in Fig. 2.3 where some data is to be added and other data is to be deducted, multiplied or divided..
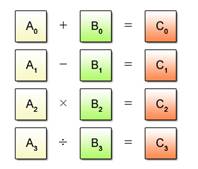
Fig. 2.3: Example of SIMD Unprocesable Patterns
2.2 Data Used in SIMD Programming
This section focuses on the data used in SIMD programming.
2.2.1 Vector Type
Conventional data types used in the C programming language, such as char, int and float, are called scalar types. Data types used for SIMD operations are called vector types. Each vector type has its corresponding scalar type as shown in Table 2.2.
Table 2.2: List of Vector Types
|
Vector Type |
Data |
|
__vector unsigned char |
Sixteen unsigned 8-bit data |
|
__vector signed char |
Sixteen signed 8-bit data |
|
__vector unsigned short |
Eight unsigned 16-bit data |
|
__vector signed short |
Eight signed 16-bit data |
|
__vector unsigned int |
Four unsigned 32-bit data |
|
__vector signed int |
Four signed 32-bit data |
|
__vector unsigned long long |
Two unsigned 64-bit data |
|
__vector signed long long |
Two signed 64-bit data |
|
__vector float |
Four single-precision floating-point data |
|
__vector double |
Two double-precision floating-point data |
2.2.2 Vector Format (Byte Order*)
The Cell uses 128-bit (16-byte) fixed-length vectors made up of 2 to 16 elements according to the data type. A vector can be interpreted as a series of scalars of the corresponding type (char, int, float and so on) in a 16-byte space. As shown in Fig. 2.4, byte ordering* and element numbering on the Cell is displayed in big-endian order.
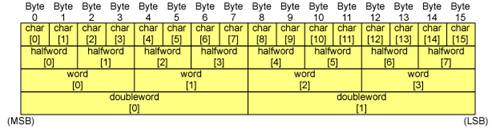
Fig. 2.4: Byte Order
* Byte Ordering: Refers to sequencing methods used when storing more than 2-byte data in computer memory. The two main types are known as big endian and little endian. In the big endian order, the most significant byte (MSB) is stored first, while in the little endian order, the least significant byte (LSB) is stored first. With big endian, for example, the 4-byte data “0x12345678” starts with 0x12 and continues through 0x34, 0x56 and 0x78. With little endian, it is recorded in reverse order, 0x78, 0x56, 0x34 and 0x12.
2.2.3 Vector Literal
A vector literal is written as a parenthesized vector type followed by a curly braced set of constant expressions. The elements of the vector are initialized to the corresponding expression. Elements for which no expressions are specified default to 0. Vector literals may be used either in initialization statements or as constants in executable statements. Some examples of usage are shown below.
Example (2-1): Use in variable initialization statement (Vector literal shown in red)
|
void func_a(void) { __vector signed int va = (__vector signed int) { -2, -1, 1, 2 };
|
Example (2-2): Use as a constant in executable statement (Vector literal shown in red)
|
va = vec_add(va, ((__vector signed int) { 1, 2, 3, 4 }));
|
When used for macros, the entire vector literal must be enclosed in parentheses.
Table 2.3 provides a list of vector literals.
Table 2.3: Vector Literals
|
Notation |
Definition |
|
(__vector unsigned char){ unsigned int,…} |
A set of sixteen unsigned 8-bit data |
|
(__vector signed char){ signed int,…} |
A set of sixteen signed 8-bit data |
|
(__vector unsigned short){ unsigned short,…} |
A set of eight unsigned 16-bit data |
|
(__vector signed short){ signed int,…} |
A set of eight signed 16-bit data |
|
(__vector unsigned int){ unsigned int,…} |
A set of four unsigned 32-bit data |
|
(__vector signed int){ signed int,…} |
A set of four signed 32-bit data |
|
(__vector unsigned long long){ unsigned long long,…} |
A set of two unsigned 64-bit data |
|
(__vector signed long long){ signed long long,…} |
A set of two signed 64-bit data |
|
(__vector float){ float,…} |
A set of four 32-bit floating-point data |
|
(__vector double){ double,…} |
A set of two 64-bit floating-point data |
2.2.4 Relationship between Vectors and Scalars
With SIMD programming, there often arises a need to refer to a specific vector element as a scalar or to refer to a block of scalars as a single vector. This section describes the referencing method to meet that need, which, for example, makes it possible to output only the third element of a vector or to bundle scalar array input data into vectors suitable for SIMD processing.
Do you remember the vector’s data structure illustrated in Fig. 2.4? Structured in the same manner as a 16-byte array of scalars and allocated in the memory as shown in Fig. 2.5, a vector (Fig. 2.5 (a)) can be viewed as a scalar array 16 bytes in data length (Fig. 2.5 (b)).
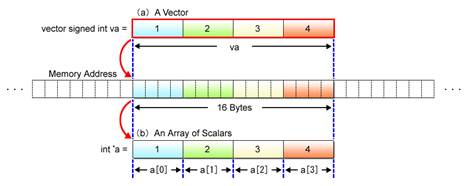
Fig. 2.5: Relationship between Scalar Array and Vector
This change in the way of looking at data is equal to pointer casting as performed in C-language programming. A vector can be referenced as a scalar by casting the vector pointer to the scalar pointer. See below for a specific example.
Example (2-3): In reference to a scalar corresponding to the third element of a vector
(Pointer cast indicated in red)
|
__vector signed int va = (__vector signed int) { 1, 2, 3, 4 }; int *a = (int *) &va;
printf(“a[2] = %d¥n”, a[2]);
|
Similarly, a scalar array in the memory can be referenced as vectors. In such cases, the scalar pointer (holding the address of the beginning of the scalar array) is cast to the vector pointer as shown in Example (2-4).
Example (2-4): In reference to vectors corresponding to a specific scalar array
(Pointer cast indicated in red)
|
int a[8] __attribute__((aligned(16))) = { 1, 2, 3, 4, 5, 6, 7, 8 }; __vector signed int *va = (__vector signed int *) a;
/* va[0] = { 1, 2, 3, 4}, va[1] = { 5, 6, 7, 8 } */ vb = vec_add(va[0], va[1]);
|
When referring to scalars in an equivalent vector form, the address of the first scalar must be aligned on a 16-byte boundary, i.e., the lower 4 bits of the address must be all “0”. If not aligned, you may not be able to refer to vector-form data in a way you expect. A visual representation of byte alignment is given in Fig. 2.6.
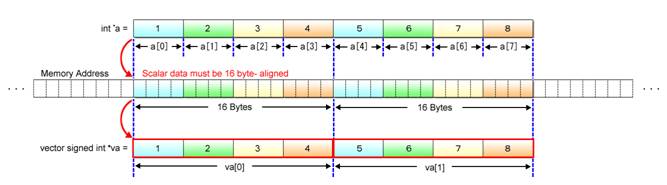
Fig. 2.6: Byte Alignment
In Example (2-4), the keyword __attribute__ is used to assign the “aligned” attribute to the scalar array a. The aligned attribute aligns data on the memory’s byte boundary.
This will be discussed in more detail in Chapter 4. For now, just keep in mind that data must be 16-byte aligned when referring to scalars as a vector.
2.3 Rudimentary SIMD Operations
This section describes SIMD operations using a summation as an example of simple arithmetic operations. We will compare SIMD operations with scalar operations and take a look into how data is handled, as well as how efficiently it is processed.
2.3.1 Program for Add Operations
Suppose that four add operations, each adding two numbers together, are required.
In such cases, conventional scalar processors use the program shown in List (2-1).
List (2-1): Scalar calculus
|
1 int a[4] = { 1, 3, 5, 7 }; 2 int b[4] = { 2, 4, 6, 8 }; 3 int c[4]; 4 5 c[0] = a[0] + b[0]; // 1 + 2 6 c[1] = a[1] + b[1]; // 3 + 4 7 c[2] = a[2] + b[2]; // 5 + 6 8 c[3] = c[3] + c[3]; // 7 + 8
|
Scalar operations are based on a rule of “single data = single data + single data”. That is, the four add instructions in the example must be executed in sequence as stated in the 5th to 8th lines of the program in order to obtain the sums for all four equations.
Next, let’s look at the SIMD program for the same operations.
List (2-2): SIMD calculus
|
1 int a[4] __attribute__((aligned(16))) = { 1, 3, 5, 7 }; 2 int b[4] __attribute__((aligned(16))) = { 2, 4, 6, 8 }; 3 int c[4] __attribute__((aligned(16))); 4 5 __vector signed int *va = (__vector signed int *) a; 6 __vector signed int *vb = (__vector signed int *) b; 7 __vector signed int *vc = (__vector signed int *) c; 8 9 *vc = vec_add(*va, *vb); // 1 + 2, 3 + 4, 5 + 6, 7 + 8
|
VMX provides built-in functions for individual SIMD instructions. In the above example, vec_add() in the 9th line indicates the built-in function corresponding to the VMX add instruction.
SIMD operations process data on the principle of “multiple data = multiple data + multiple data”. This means that SIMD operations can process a greater quantity of data per instruction than scalar operations, making it possible to reduce the number of instructions necessary to be executed and thus the time required for processing.
As explained in Section 2.2, arrays a, b and c are referenced as vectors. To make them 16-byte aligned, therefore, the aligned attribute is assigned by using the keyword __attribute__.
2.3.2 Sample Program
The following illustrates the entire source code you need to write for the above add operations.
Sample Program (2-1): Overall structure of the program for add operations
|
1 #include <stdio.h> 2 #include <altivec.h> 3 4 int a[4] __attribute__((aligned(16))) = { 1, 3, 5, 7 }; 5 int b[4] __attribute__((aligned(16))) = { 2, 4, 6, 8 }; 6 int c[4] __attribute__((aligned(16))); 7 8 int main(int argc, char **argv) 9 { 10 __vector signed int *va = (__vector signed int *) a; 11 __vector signed int *vb = (__vector signed int *) b; 12 __vector signed int *vc = (__vector signed int *) c; 13 14 *vc = vec_add(*va, *vb); // 1 + 2, 3 + 4, 5 + 6, 7 + 8 15 16 printf("c[0]=%d, c[1]=%d, c[2]=%d, c[3]=%d¥n", c[0], c[1], c[2], c[3]); 17 18 return 0; 19 }
|
Line 2 Used to include the header file “altivec.h” necessary for utilizing VMX instructions. The character stream “altivec” will be found not only in the header file but also in other files as VMX instructions are grounded in the AltiVec technology.
Lines 4 〜6 Used to define the input array data a and b, as well as the scalar array c used to store the sums. Addresses of these variables are 16-byte aligned using the aligned attribute.
Lines 10 〜12 Used to define the variables necessary for SIMD processing. Variables va, vb and vc are pointers to the vector variables used in SIMD operations. They allow scalar arrays to be referred to in the vector form.
Line 14 Used to execute the vec_add() function to enable add instruction execution. This function makes it possible to add the values in the corresponding elements of va and vb and store the results in the elements of vc.
Line 16 Used to display the results on the standard output.
2.3.3 Program Compiling and Execution
To compile the program, use the gcc command. With VMX, the -maltivec and -mabi=altivec compile options must also be specified.
Example (2-5): Program compilation
|
$ gcc -maltivec -mabi=altivec vec_add.c -o vec_add.elf
|
Program execution by using VMX instructions is no different from the conventional method. At the shell prompt, run the ELF executable file.
Example (2-6): Program execution
|
$ ./vec_add.elf c[0]=3, c[1]=7, c[2]=11, c[3]=15 $
|
2.3.4 Built-in Functions for VMX Instructions (Intrinsics)
So far, the vec_add() function corresponding to the VMX add instruction has been explained. A variety of other built-in functions are also available for VMX instructions for use in arithmetic operations, bit operations and comparison operations. Some of them are listed in Table 2.4.
Table 2.4: Built-in Functions for VMX Instructions (Representative Examples)
|
Applicable Instructions |
Function Name |
Description |
|
Arithmetic Instructions |
vec_add(a, b) |
Adds the elements of vectors a and b. |
|
vec_sub(a, b) |
Performs subtractions between the elements of vectors a and b. |
|
|
vec_madd(a, b, c) |
Multiplies the elements of vector a by the elements of vector b and adds the elements of vector c. |
|
|
vec_re(a) |
Calculates the reciprocals of the elements of vector a. |
|
|
vec_rsqrte(a) |
Calculates the square roots of the reciprocals of the elements of vector a. |
|
|
Logical Instructions |
vec_and(a, b) |
Finds the bitwise logical products (AND) between vectors a and b. |
|
vec_or(a, b) |
Finds the bitwise logical sums (OR) between vectors a and b. |
|
|
Shift/Rotate Instructions |
vec_sr(a, b) |
Right-shifts the elements of vector a in accordance with the number of bits specified by the elements of vector b. |
|
vec_rl(a, b) |
Left-rotates the elements of vector a in accordance with the number of bits specified by the elements of vector b. |
|
|
Bit Operation Instructions |
vec_perm(a, b, c) |
Realigns the elements of vectors a and b so that they match the byte pattern specified by vector c. |
|
vec_sel(a, b, c) |
Selects the bits in vectors a and b according to the bit pattern specified by vector c. |
|
|
Compare Instructions |
vec_cmpeq(a, b) |
Compares if the elements of vector a are equal to the elements of vector b. |
|
vec_cmpgt(a, b) |
Checks if the elements of vector a are numerically greater than those of vector b. |
|
|
Conversion Instructions |
vec_ctf(a, b) |
Divides the elements of integer vector a by 2b and converts them into floating-point values. |
|
vec_ctu(a, b) |
Multiplies the elements of floating-point vector a by 2b and converts them into unsigned integers. |
|
|
Constant Generation Instructions |
vec_splat(a, b) |
Generates a new vector by expanding the bth element of vector a. |
|
vec_splat_s32(a) |
Generates a new vector by expanding the scalar literal a into four signed 32-bit equivalent data. |
2.3.5 Reference Document
Table 2.4 shows typical VMX intrinsic functions only. If you need more information, please refer to Chapter 4 of Freescale Semiconductor’s “AltiVec Technology Programming Interface Manual”.
(http://www.freescale.com/files/32bit/doc/ref_manual/ALTIVECPIM.pdf?srch=1)
2.4 Generation of SIMD-Ready Vectors
SIMD operations almost always use scalar arrays as input data. However, the data structure of these arrays is not always suited for SIMD operations. That’s why this section has been provided to explain how to change such inputs into SIMD-ready vectors.
2.4.1 Need for Data Realignment
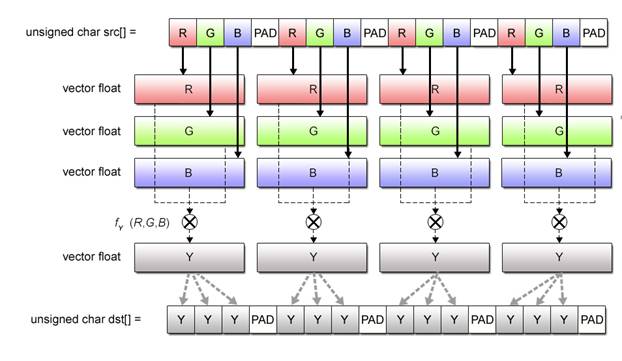
Typical examples of data that may not be suitable for SIMD operations include color data of images and 3-dimensional data for 3D graphics. Take, for example, the case of computing the brightness Y of each pixel from its RGB values. The formula used for this calculation is as follows.
(Brightness calculation formula) Y = R x 0.29891 + G x 0.58661 + B x 0.11448
SIMD calculation of brightness using this formula requires the use of data grouped into R, G and B vectors as illustrated in Fig. 2.7.
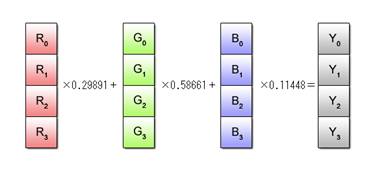
Fig. 2.7: Brightness Computation by SIMD Operations
Most often, however, color data read out from an image file is configured in RGB units as shown in Fig. 2.7 (a) and thus is not appropriate for SIMD operations. It must be realigned into vectors as shown in Fig. 2.8 (b).
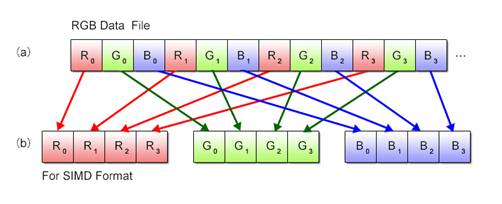
Fig. 2.8: Realignment of RGB Data
2.4.2 Vector Realignment Mechanism
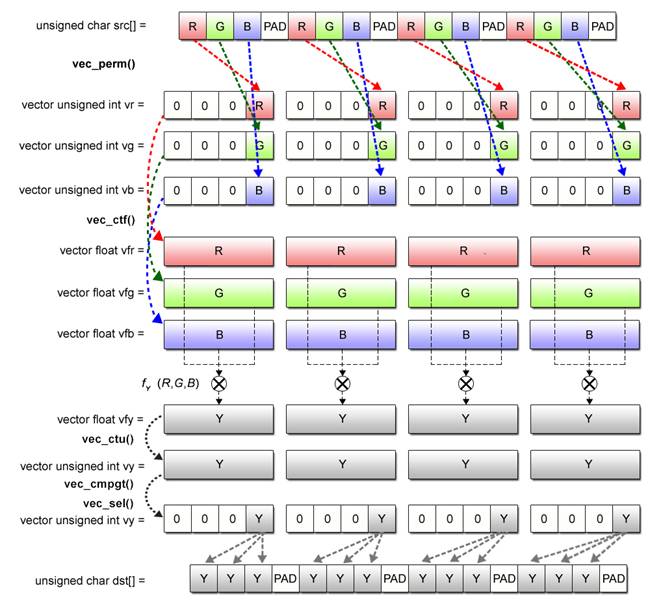
Now then, let’s examine how realignment can actually be performed. With SIMD operations, the built-in function vec_perm() is used for this purpose. Using three arguments – two vectors to be realigned plus a realignment pattern, this function generates a new vector and returns it as the function value.
Example (2-7): Description of the vec_perm() function
|
vc = vec_perm(va, vb, vpat);
|
For the first and second arguments va and vb, specify the vectors subject to realignment. For the third argument vpat, specify the realignment pattern. Each byte in the realignment pattern represents the element number when the two vectors are assumed to be linked together to form a single 32-byte array. Fig. 2.9 depicts an image of processing using the vec_perm() function.
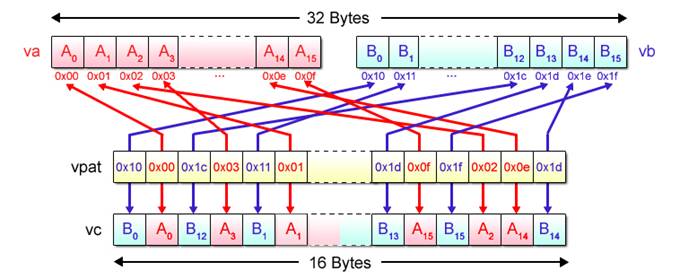
Fig. 2.9: Processing by vec_perm Function (Image)
2.4.3 Program for Matrix Transposition
An example of obtaining a transposed matrix is shown below.
Matrix A comprised of m rows by n columns can be transposed to another matrix comprised of n rows by m columns by interchanging the elements Aij and Aji of the matrix A. The n-by-m matrix produced in this way is described as AT. It is used mainly for coordinate transformations in 3D graphics processing.
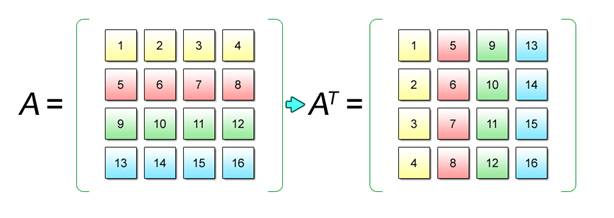
Fig. 2.10: Matrix Transposition
The following demonstrates how to transpose the 4x4 matrix shown in Fig. 2.10, using the vec_perm() function.
List (2-3): Program to transpose a 4x4 matrix
|
1 int a[16] __attribute__((aligned(16))) = { 1, 2, 3, 4, 2 5, 6, 7, 8, 3 9, 10, 11, 12, 4 13, 14, 15, 16 }; 5 int aT[16] __attribute__((aligned(16))); 6 7 __vector signed int *va = (__vector signed int *) a; 8 __vector signed int *vaT = (__vector signed int *) aT; 9 __vector signed int vtmp[4]; 10 __vector unsigned char vpat1 = (__vector unsigned char) { 0x00, 0x01, 0x02, 0x03, 11 0x04, 0x05, 0x06, 0x07, 12 0x10, 0x11, 0x12, 0x13, 13 0x14, 0x15, 0x16, 0x17 }; 14 __vector unsigned char vpat2 = (__vector unsigned char) { 0x08, 0x09, 0x0a, 0x0b, 15 0x0c, 0x0d, 0x0e, 0x0f, 16 0x18, 0x19, 0x1a, 0x1b, 17 0x1c, 0x1d, 0x1e, 0x1f }; 18 __vector unsigned char vpat3 = (__vector unsigned char) { 0x00, 0x01, 0x02, 0x03, 19 0x10, 0x11, 0x12, 0x13, 20 0x08, 0x09, 0x0a, 0x0b, 21 0x18, 0x19, 0x1a, 0x1b }; 22 __vector unsigned char vpat4 = (__vector unsigned char) { 0x04, 0x05, 0x06, 0x07, 23 0x14, 0x15, 0x16, 0x17, 24 0x0c, 0x0d, 0x0e, 0x0f, 25 0x1c, 0x1d, 0x1e, 0x1f }; 26 27 vtmp[0] = vec_perm(va[0], va[2], vpat1); 28 vtmp[1] = vec_perm(va[1], va[3], vpat1); 29 vtmp[2] = vec_perm(va[0], va[2], vpat2); 30 vtmp[3] = vec_perm(va[1], va[3], vpat2); 31 32 vaT[0] = vec_perm(vtmp[0], vtmp[1], vpat3); 33 vaT[1] = vec_perm(vtmp[0], vtmp[1], vpat4); 34 vaT[2] = vec_perm(vtmp[2], vtmp[3], vpat3); 35 vaT[3] = vec_perm(vtmp[2], vtmp[3], vpat4);
|
This example uses four vector variables per matrix because each element of the matrix is 4 bytes long. Also, the transpose of vector variables takes place in two steps as shown in Fig. 2.11 because only two variables can be interchanged per the execution of the vec_perm() function, making it necessary to repeat the same operation a total of eight times to turn all rows into columns.
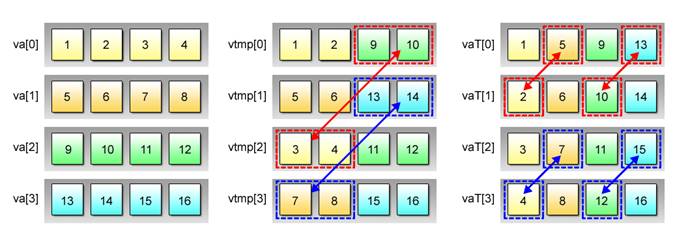
Fig. 2.11: Two-Tiered Transpose Operation
2.4.4 Sample Program
The following shows the entire source code you need to write for the above transpose program.
Sample Program (2-2): Matrix transpose program
|
1 #include <stdio.h> 2 #include <altivec.h> 3 4 int a[16] __attribute__((aligned(16))) = { 1, 2, 3, 4, 5 5, 6, 7, 8, 6 9, 10, 11, 12, 7 13, 14, 15, 16 }; 8 int aT[16] __attribute__((aligned(16))); 9 10 void print_matrix(int *matrix) 11 { 12 int i, j; 13 14 for (i = 0; i < 4; i++) { 15 for (j = 0; j < 4; j++) { 16 printf("%2d ", matrix[i * 4 + j]); 17 } 18 printf("¥n"); 19 } 20 return; 21 } 22 23 int main(int argc, char **argv) 24 { 25 __vector signed int *va = (__vector signed int *) a; 26 __vector signed int *vaT = (__vector signed int *) aT; 27 __vector signed int vtmp[4]; 28 __vector unsigned char vpat1 = (__vector unsigned char) { 0x00, 0x01, 0x02, 0x03, 29 0x04, 0x05, 0x06, 0x07, 30 0x10, 0x11, 0x12, 0x13, 31 0x14, 0x15, 0x16, 0x17 }; 32 __vector unsigned char vpat2 = (__vector unsigned char) { 0x08, 0x09, 0x0a, 0x0b, 33 0x0c, 0x0d, 0x0e, 0x0f, 34 0x18, 0x19, 0x1a, 0x1b, 35 0x1c, 0x1d, 0x1e, 0x1f }; 36 __vector unsigned char vpat3 = (__vector unsigned char) { 0x00, 0x01, 0x02, 0x03, 37 0x10, 0x11, 0x12, 0x13, 38 0x08, 0x09, 0x0a, 0x0b, 39 0x18, 0x19, 0x1a, 0x1b }; 40 __vector unsigned char vpat4 = (__vector unsigned char) { 0x04, 0x05, 0x06, 0x07, 41 0x14, 0x15, 0x16, 0x17, 42 0x0c, 0x0d, 0x0e, 0x0f, 43 0x1c, 0x1d, 0x1e, 0x1f }; 44 45 printf("--- original matrix ---¥n"); 46 print_matrix(a); 47 48 /* vec_perm() part 1 */ 49 vtmp[0] = vec_perm(va[0], va[2], vpat1); 50 vtmp[1] = vec_perm(va[1], va[3], vpat1); 51 vtmp[2] = vec_perm(va[0], va[2], vpat2); 52 vtmp[3] = vec_perm(va[1], va[3], vpat2); 53 54 printf("--- transform 1 ---¥n"); 55 print_matrix((int *) vtmp); 56 57 /* vec_perm() part 2 */ 58 vaT[0] = vec_perm(vtmp[0], vtmp[1], vpat3); 59 vaT[1] = vec_perm(vtmp[0], vtmp[1], vpat4); 60 vaT[2] = vec_perm(vtmp[2], vtmp[3], vpat3); 61 vaT[3] = vec_perm(vtmp[2], vtmp[3], vpat4); 62 63 printf("--- transform 2 ---¥n"); 64 print_matrix(aT); 65 66 return 0; 67 }
|
Lines 4〜8 Used to define the matrix a and the transposed matrix aT in terms of scalar arrays.
Lines 10〜21 Used to define the function for outputting the matrix to the standard output.
Lines 25〜27 Used to define the variables necessary for SIMD operations. Variables va and vaT are pointers to the vector variables used in SIMD operations. These variables allow referencing to scalar arrays in the vector form. The vector variable array vtmp needs to be defined to retain the interim result during the two-step realignment operations of vector variables.
Lines 28〜43 Used to define the vector variable realignment pattern for the transpose. The first step realignment uses vpat1 and vpat2, while the second, vpat3 and vpat4.
Lines 45〜46 Used to output the content of the matrix a to the standard output.
Lines 49〜55 Used to execute the first-step realignment operation, as well as to output the interim result vtmp to the standard output.
Lines 58〜64 Used to execute the second-step realignment operation, as well as to output the transposed matrix aT to the standard output.
2.5 Elimination of Conditional Branches
With scalar operations, a conditional branch is used to alter the processing flow when a specified condition is met. The use of branch instructions, however, affects the efficiency of SIMD operations because it requires decomposing each vector into elements and processing them sequentially. SIMD processors therefore employ another method to obtain the same result as conditional branching.
2.5.1 Branch-Equivalent SIMD Processing
When different operations have to be performed according to set conditions, scalar processors first evaluate the given condition as shown in Fig. 2.12 (a) and take the appropriate branch according to the result of the evaluation. SIMD processors provide the equivalent of this operation, while maintaining their primary efficiency, by following the sequence described in Fig. 2.12 (b).
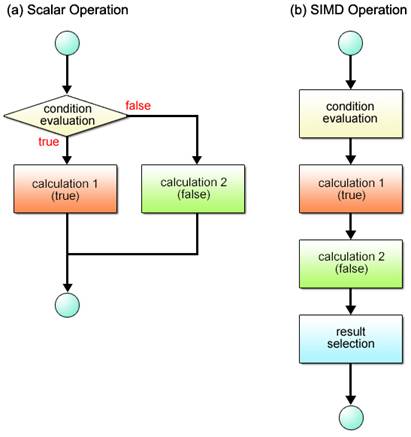
Fig. 2.12: Conditional Branch Processing Flows
Here are the details of the procedure illustrated in Fig. 2.12 (b).
To begin with, an authenticity check is performed as shown in Fig. 2.13 to determine if the condition holds true or not.
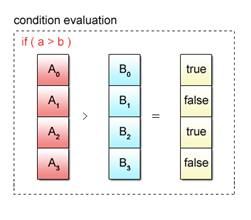
Fig. 2.13: Condition Evaluation
Next, calculations are executed for both true and false condition cases as shown in Fig. 2.14.
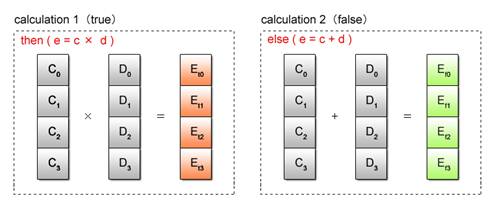
Fig. 2.14: Condition-Based Dual Calculations
Of the two outcomes obtained per vector element, the one that conforms to the result of the condition evaluation is selected and stored. This selective storing of the outcome is performed for all vector elements, simultaneously by a single operation, as shown in Fig. 2.15.
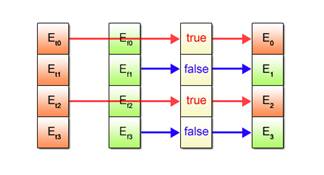
Fig. 2.15: Selection of Processed Results
In sum, SIMD operations provide the same result as forming a conditional branch by selecting between the outcomes of calculations performed for both true and false condition states.
2.5.2 Comparison and Selection
Now then, let’s proceed to the exact method of eliminating conditional branching.
SIMD operations eliminate conditional branching by using a compare instruction and a bit select instruction. More specifically, a built-in function corresponding to the compare instruction of, for example, the vec_cmpgt() function is used for condition evaluation in the beginning. For processed result selection, the vec_sel() function related to the bit select instruction is used.
After comparing the element of the first argument va with the corresponding element of the second argument vb, the vec_cmpgt() function generates and returns a new vector with all bits of the corresponding element set to “1”(if the element of va is numerically greater than that of vb)or to “0” (otherwise).
Example (2-8): Description of the vec_cmpgt() function
|
vpat = vec_cmpgt(va, vb);
|
Fig. 2.16 depicts an image of processing performed by the vec_cmpgt() function.
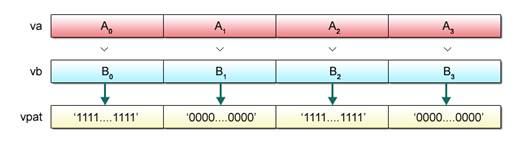
Fig. 2.16: Processing by vec_cmpgt() Function (Image)
The vec_sel() function generates and returns a vector based on the 128-bit selection pattern specified by the third argument vpat. This function selects the bits of the first argument va if the vpat bits are all “0”. Alternatively, it selects the bits of the second argument vb if the vpat bits are all “1”.
Example (2-9): Description of the vec_sel() function
|
vc = vec_sel(va, vb, vpat);
|
Fig. 2.17 provides an overall picture of the operations performed by the use of the vec_cmpgt() and vec_sel() functions.
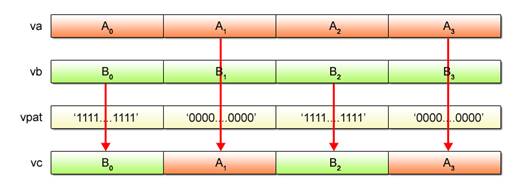
Fig. 2.17: Processing by vec_cmpgt() and vec_sel() Functions (Image)
2.5.3 Program for Absolute Difference Computation
Shown below is the sample program for calculating the absolute value of the difference between the values of two elements, taken to review the conditional branching described heretofore in Section 5.
List (2-4): Scalar program for difference calculation
|
1 int a[16] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 }; 2 int b[16] = { 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 }; 3 int c[16]; 4 5 int i; 6 7 for (i = 0; i < 16; i++) { 8 if (a[i] > b[i]) { 9 c[i] = a[i] - b[i]; 10 } else { 11 c[i] = b[i] - a[i]; 12 } 13 }
|
This program repeats comparisons between the elements of scalar arrays a and b. With each comparison made, b[i] is subtracted from a[i] if the element of the array a is numerically greater than that of the array b. For a set of a and b elements in reverse relationship, a[i] is subtracted from b[i]. A conditional branch is used every time a subtraction is performed.
The SIMD program applicable to the same purpose is as follows. The program uses the function vec_cmpgt() for comparisons of values.
List (2-5): SIMD program for difference calculation
|
1 int a[16] __attribute__((aligned(16))) = { 1, 2, 3, 4, 5, 6, 7, 8, 2 9, 10, 11, 12, 13, 14, 15, 16 }; 3 int b[16] __attribute__((aligned(16))) = { 16, 15, 14, 13, 12, 11, 10, 9, 4 8, 7, 6, 5, 4, 3, 2, 1 }; 5 int c[16] __attribute__((aligned(16))); 6 7 __vector signed int *va = (__vector signed int *) a; 8 __vector signed int *vb = (__vector signed int *) b; 9 __vector signed int *vc = (__vector signed int *) c; 10 __vector signed int vc_true, vc_false; 11 __vector unsigned int vpat; 12 13 for (i = 0; i < 4; i++) { 14 vpat = vec_cmpgt(va[i], vb[i]); 15 vc_true = vec_sub(va[i], vb[i]); 16 vc_false = vec_sub(vb[i], va[i]); 17 vc[i] = vec_sel(vc_false, vc_true, vpat); 18 }
|
Unlike scalar operations, conditional branching is unnecessary. Instead, all four element values are compared simultaneously, with subtractions performed for both true and false condition states. Then one of the two difference values obtained for each element, which is compliant with the result of condition evaluation, is selected and stored in the vector variable vc.
2.5.4 Sample Program
The following shows the entire source code you need to write for the SIMD program explained in Section 2.5.3.
Sample Program (2-3): Overall structure of the program for difference calculation
|
1 #include <stdio.h> 2 #include <altivec.h> 3 4 int a[16] __attribute__((aligned(16))) = { 1, 2, 3, 4, 5, 6, 7, 8, 5 9, 10, 11, 12, 13, 14, 15, 16 }; 6 int b[16] __attribute__((aligned(16))) = { 16, 15, 14, 13, 12, 11, 10, 9, 7 8, 7, 6, 5, 4, 3, 2, 1 }; 8 int c[16] __attribute__((aligned(16))); 9 10 int main(int argc, char **argv) 11 { 12 __vector signed int *va = (__vector signed int *) a; 13 __vector signed int *vb = (__vector signed int *) b; 14 __vector signed int *vc = (__vector signed int *) c; 15 __vector signed int vc_true, vc_false; 16 __vector unsigned int vpat; 17 18 int i; 19 20 for (i = 0; i < 4; i++) { 21 vpat = vec_cmpgt(va[i], vb[i]); 22 vc_true = vec_sub(va[i], vb[i]); 23 vc_false = vec_sub(vb[i], va[i]); 24 vc[i] = vec_sel(vc_false, vc_true, vpat); 25 } 26 27 for (i = 0; i < 16; i++) { 28 printf("c[%02d]=%2d¥n", i, c[i]); 29 } 30 31 return 0; 32 }
|
Lines 4〜8 Used to define the input array data a and b, plus the scalar array c for storing the derived difference values.
Lines 12〜16 Used to define the variables necessary for SIMD operations. Variables va, vb and vc are pointers to the vector variables used in SIMD operations. These variables allow referencing to scalar arrays in an equivalent vector form.
Lines 20〜25 The for loop performs numeric comparison between the elements of va and vb, as well as difference calculations for both true and false conditions, and stores the results in variables vc_true and vc_false. The vec_sel() function allows selection from these difference values for storage in the variable vc.
Lines 27〜29 Used to output the difference values to the standard output.
2.6 Exercise (2-1): Total Calculation Program
Here is a review question about what we’ve learned in Section 2.3.
|
【Question】
Practice Program (2-1) is a program for finding the sum total of 1 to 1024. Rewrite this program so that it can perform SIMD operations.
The program uses the for statement to add individual numbers to the variable sum, while incrementing the int variable i.
|
|
【Practice Program(2-1)】
1 #include <stdio.h> 2 3 #define MAX_NUM (1024) 4 5 int main(int argc, char **argv) 6 { 7 int i; 8 int sum = 0; 9 10 for (i = 1; i <= MAX_NUM; i++) { 11 sum += i; 12 } 13 14 printf("sum: %d¥n", sum); 15 16 return 0; 17 }
|
|
【Strategy to Obtain the Answer】
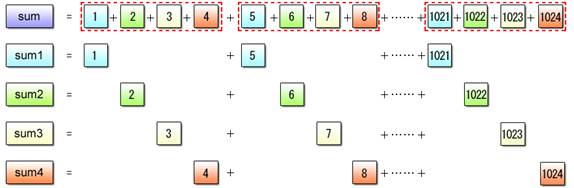
The focus of discussion here is on how to divide the data and how to process it with SIMD operations. Since the data type is int, SIMD operations can handle four values at a time. Accordingly, divide the data (numbers from 1 to 1024) into four segments, calculate the partial sums for these segments and add the four partial sums together at the end.
Follow the steps below to work out the solution program.
(1) Perform a four-way data split and use SIMD operations to calculate four partial sums.
Fig. 2.18: Partial Sum Calculation
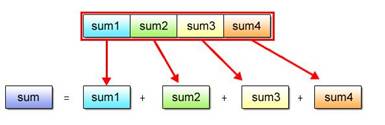
(2) Calculate the total sum value, making reference to the four partial sums in the scalar form. Pointer-cast as described in Section 2.2 to refer to the partial sums.
Fig. 2.19: Totaling Partial Sums
|
A model solution is provided below, together with brief explanations of the program and the source code.
|
【Solution Program (2-1)】
1 #include <stdio.h> 2 #include <altivec.h> 3 4 #define MAX_NUM (1024) 5 6 int main(int argc, char **argv) 7 { 8 int i; 9 int sum; 10 int *psum; 11 12 __vector signed int va = (__vector signed int) { 1, 2, 3, 4 }; 13 __vector signed int vsum = (__vector signed int) { 0, 0, 0, 0 }; 14 __vector signed int vstep = (__vector signed int) { 4, 4, 4, 4 }; 15 16 for (i = 1; i <= MAX_NUM; i += 4) { 17 vsum = vec_add(vsum, va); 18 va = vec_add(va, vstep); 19 } 20 21 psum = (int *) &vsum; 22 sum = psum[0] + psum[1] + psum[2] + psum[3]; 23 24 printf("sum: %d¥n", sum); 25 26 return 0; 27 }
|
|
【Program Description】
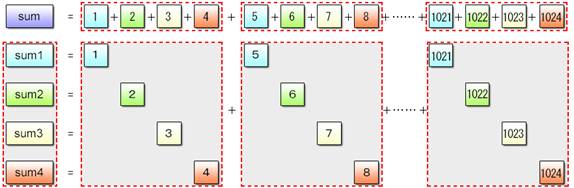
This program is one of the applied examples of Sample Program (2-1). To calculate partial sums, it makes use of the vec_add() function that sequentially adds the vector variable va to the vector variable vsum. The vector variable va is initialized with { 1, 2, 3, 4 } and incremented by 4 using the vector variable vstep on each iteration.
Fig. 2.20: SIMD Partial Sum Computation
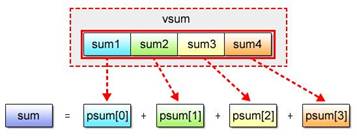
Upon completion of partial sum calculations, perform a pointer cast so that the vector variable vsum containing the partial sum data can be interpreted as the scalar array psum, making it possible to obtain the inclusive sum by totaling the elements of this array
Fig. 2.21: Adding Partial Sums (Pointer Cast)
The source code included in the above solution program is as follows.
Lines 12〜14 Used to furnish vector variables va, vsum and vstep. In the practice program, the scalar variable i functions both as a counter and data. In the solution program, however, it assumes the role of the counter only. Line 17 Using the vec_add() function, calculates the sum value vsum. Line 18 Using the vec_add() function, increments va for the equivalent of vstep. Lines 21〜22 Allow calculation of the inclusive sum by making it possible to refer to scalars corresponding to the elements of the vector stored in the variable vsum.
|
2.7 Exercise (2-2): Floating-Point Calculation Program
Here is a review question about what we’ve learned in Section 2.4.
|
【Question】
Practice Program (2-2) is a program for multiplying integers 1 to 16 individually by 0.1. Rewrite this program so that it can perform SIMD operations.
Integer values 1 to 16 in this program are given in the form of the scalar unsigned short array in. The result of floating-point calculations is stored in the scalar float array out.
|
|
【Practice Program (2-2)】
1 #include <stdio.h> 2 3 #define SIZE (16) 4 5 unsigned short in[SIZE] = { 1, 2, 3, 4, 5, 6, 7, 8, 6 9, 10, 11, 12, 13, 14, 15, 16 }; 7 float out[SIZE]; 8 9 int main(int argc, char **argv) 10 { 11 int i; 12 13 for (i = 0; i < SIZE; i++) { 14 out[i] = (float) in[i] * 0.1f; 15 } 16 17 for (i = 0; i < SIZE; i++) { 18 printf("out[%02d]=%0.1f¥n", i, out[i]); 19 } 20 21 return 0; 22 }
|
|
【Strategy to Obtain the Answer】
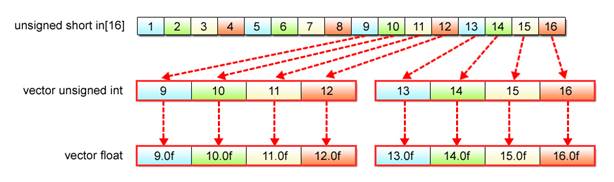
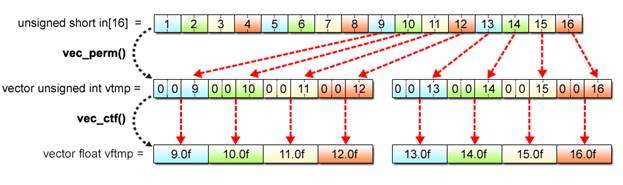
The biggest challenge here is how to change the vector data type by SIMD operations. The given data, which is unsigned short, must be converted into float data to allow floating-point calculations. With SIMD operations, this is performed by the use of the vec_ctf() function.
The use of the vec_ctf() function, however, gives rise to a need for another data type conversion. Since this function can take arguments in the form of 32-bit unsigned int vectors only, conversion from 16-bit unsigned short to 32-bit unsigned int data also becomes necessary. With SIMD operations, the unsigned short to unsigned int conversion is executed based on the vector realignment mechanism explained in Section 2.4.
Fig. 2.22: unsigned short to float Conversion
|
A model solution is provided below, together with brief explanations of the program and the source code.
|
【Solution Program (2-2)】
1 #include <stdio.h> 2 #include <altivec.h> 3 4 #define SIZE (16) 5 6 unsigned short in[SIZE] __attribute__((aligned(16))) = { 1, 2, 3, 4, 5, 6, 7, 8, 7 9, 10, 11, 12, 13, 14, 15, 16 }; 8 float out[SIZE] __attribute__((aligned(16))); 9 10 int main(int argc, char **argv) 11 { 12 int i; 13 14 __vector unsigned short *vin = (__vector unsigned short *) in; 15 __vector float *vout = (__vector float *) out; 16 __vector unsigned char vpat1 = (__vector unsigned char) { 0x10, 0x10, 0x00, 0x01, 17 0x10, 0x10, 0x02, 0x03, 18 0x10, 0x10, 0x04, 0x05, 19 0x10, 0x10, 0x06, 0x07 }; 20 __vector unsigned char vpat2 = (__vector unsigned char) { 0x10, 0x10, 0x08, 0x09, 21 0x10, 0x10, 0x0a, 0x0b, 22 0x10, 0x10, 0x0c, 0x0d, 23 0x10, 0x10, 0x0e, 0x0f }; 24 __vector unsigned int vtmp; 25 __vector float vftmp; 26 __vector unsigned short vzero = (__vector unsigned short) { 0, 0, 0, 0, 0, 0, 0, 0 }; 27 __vector float vfzero = (__vector float) { 0.0f, 0.0f, 0.0f, 0.0f }; 28 __vector float vtenth = (__vector float) { 0.1f, 0.1f, 0.1f, 0.1f }; 29 30 for (i = 0; i < SIZE/8; i++) { 31 vtmp = vec_perm(vin[i], vzero, vpat1); 32 vftmp = vec_ctf(vtmp, 0); 33 vout[i*2] = vec_madd(vftmp, vtenth, vfzero); 34 35 vtmp = vec_perm(vin[i], vzero, vpat2); 36 vftmp = vec_ctf(vtmp, 0); 37 vout[i*2+1] = vec_madd(vftmp, vtenth, vfzero); 38 } 39 40 for (i = 0; i < SIZE; i++) { 41 printf("out[%02d]=%0.1f¥n", i, out[i]); 42 } 43 44 return 0; 45 }
|
2.8 Exercise (2-3): Absolute Value Calculation Program
Here is a review question about what we’ve learned in Section 2.5.
|
【Question】
Practice Program (2-3) shown below is used to obtain the absolute values for 16 real numbers defined in a scalar array. Rewrite this program so that it can perform SIMD operations.
As to the 16 signed numbers contained as array elements, this program checks whether they are positive or negative and inverts the negative ones.
Input data is provided in the form of a 16-element scalar array in. The absolute value of each element is stored as output data in the scalar array out.
|
|
【Practice Program (2-3)】
1 #include <stdio.h> 2 3 #define SIZE (16) 4 5 float in[SIZE] = { 1, -2, 3, -4, 6 5, -6, 7, -8, 7 9, -10, 11, -12, 8 13, -14, 15, -16 }; 9 float out[SIZE]; 10 11 int main(int argc, char **argv) 12 { 13 int i; 14 15 for (i = 0; i < SIZE; i++) { 16 if (in[i] > 0) { 17 out[i] = in[i]; 18 } else { 19 out[i] = in[i] * -1; 20 } 21 } 22 23 for (i = 0; i < SIZE; i++) { 24 printf("out[%02d]=%0.0f¥n", i, out[i]); 25 } 26 27 return 0; 28 }
|
|
【Strategy to Obtain the Answer】
As explained in Section 2.5, the first priority must be given to the elimination of conditional branching that negatively affects the efficiency of SIMD operations.
A built-in function vec_abs() is available for absolute value calculations. However, please try to write your program without using this function.
|
A model solution is provided below, together with brief explanations of the program and the source code.
|
【Solution Program (2-3)】
1 #include <stdio.h> 2 #include <altivec.h> 3 4 #define SIZE (16) 5 6 float in[SIZE] __attribute__((aligned(16))) = { 1, -2, 3, -4, 7 5, -6, 7, -8, 8 9, -10, 11, -12, 9 13, -14, 15, -16 }; 10 float out[SIZE] __attribute__((aligned(16))); 11 12 int main(int argc, char **argv) 13 { 14 int i; 15 16 __vector float *vin = (__vector float *) in; 17 __vector float *vout = (__vector float *) out; 18 __vector float vin_negative; 19 __vector unsigned int vpat; 20 21 __vector float vzero = (__vector float) { 0.0f, 0.0f, 0.0f, 0.0f }; 22 __vector float vminus = (__vector float) { -1.0f, -1.0f, -1.0f, -1.0f }; 23 24 for (i = 0; i < SIZE/4; i++) { 25 vpat = vec_cmpgt(vin[i], vzero); 26 vin_negative = vec_madd(vin[i], vminus, vzero); 27 vout[i] = vec_sel(vin_negative, vin[i], vpat); 28 } 29 30 for (i = 0; i < SIZE; i++) { 31 printf("out[%02d]=%0.0f¥n", i, out[i]); 32 } 33 34 return 0; 35 }
|
|
【Program Description】
This program is an applied example of Sample Program (2-3). With each value contained in the input array vin, positive/negative detection is performed and the detected result is stored in vpat. Next, the sign-inverted value vin_negative is calculated and last of all, selection between the vin and vin_negative array elements is performed by the vec_sel() function based on which element vpat points to.
The source code used in the above solution program is as follows.
Lines 16〜17 Used to enable scalar to vector pointer cast, making it possible to refer to scalar arrays in and out in an equivalent vector form. Lines 18〜22 Used to define the vector variable vin_negative to enable sign inversion. Line 25 As to each element in vin, determines whether it is greater than “0” or not, using the vec_cmpgt() function. Line 26 Used to calculate the vin_negative value (vin multiplied by -1). Line 27 Using the vec_sel() function, selects absolute values (positive values) only and stores them in the output data array out.
|
2.9 Exercise (2-4): Grayscale Conversion Program
This program is included so that you can test your comprehension of the information contained in Chapter 2.
|
【Question】
Practice Program (2-4) shows a code snippet taken from a program used to convert color images into grayscale images. More precisely, it displays the rgb2y() function that undertakes grayscale conversion. Rewrite this function so that it can perform SIMD operations.
Grayscale conversion involves extraction of brightness data Y from each pixel’s RGB values to make it possible to render images composed of shades of gray. The formula used for brightness calculation is shown below.
(Brightness calculation formula) fY(R, G, B) = R x 0.29891 + G x 0.58661 + B x 0.11448
Fig. 2.24: Grayscale Conversion
The first and second arguments src and dst of the rgb2y() function hold the values of the pointers to the input buffer (color image) and the output buffer (grayscale image) respectively. The number of pixels to be processed is passed to the third argument num.
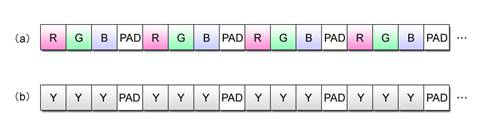
The input data to be passed to the rgb2y() function is configured as shown in Fig. 2.25 (a). After going through the grayscale conversion process, the data is output in the format shown in Fig. 2.25 (b). An 8-bit unsigned integer is stored in each element of both input and output.
Fig. 2.25: Data Format
In addition, the value of each product obtained is rounded at the maximum value of 255 in order to prevent the RGB value overflow that may be caused by floating-point calculation errors.
|
|
【Practice Program (2-4)】(Partial Excerpt)
1 #include <stdio.h> 2 3 void rgb2y(unsigned char *src, unsigned char *dst, int num) 4 { 5 int i; 6 float r, g, b, y; 7 float rconst = 0.29891f; 8 float gconst = 0.58661f; 9 float bconst = 0.11448f; 10 unsigned int max = 255; 11 12 for (i = 0; i < num; i++) { 13 r = (float) src[i * 4]; 14 g = (float) src[i * 4 + 1]; 15 b = (float) src[i * 4 + 2]; 16 17 y = r * rconst + g * gconst + b * bconst; 18 19 if (y > max) { 20 y = max; 21 } 22 23 dst[i * 4] = dst[i * 4 + 1] = dst[i * 4 + 2] = (unsigned char) y; 24 } 25 26 return; 27 }
|
|
【Strategy to Obtain the Answer】
This program involves all the important aspects of programming covered by previously introduced sample programs and practice programs. Brightness calculation not only calls for the conversion from unsigned char RGB values to float data but also requires floating-point calculations. In addition, elimination of conditional branches is necessary when using SIMD operations to round off floating-point calculation errors. With all this in mind, proceed as follows to create a solution program.
(1) For the convenience of SIMD operations, realign color data in groups of R, G and B elements. (2) Perform __vector unsigned char to __vector float conversion on the realigned data in order to allow floating-point calculations for brightness data. You have already experienced this conversion of data type in Practice Program (2-2). (3) Brightness values obtained as the result of calculation are output to the output buffer in the form of { Y, Y, Y, 0 }.
Fig. 2.26: RGB to Grayscale Conversion
|
A model solution is provided below, together with brief explanations of the program and the source code.
|
【Solution Program (2-4)】
1 #include <stdio.h> 2 #include <altivec.h> 3 4 void rgb2y(unsigned char *src, unsigned char *dst, int num) 5 { 6 int i; 7 8 __vector unsigned char *vsrc = (__vector unsigned char *) src; 9 __vector unsigned char *vdst = (__vector unsigned char *) dst; 10 11 __vector unsigned int vr, vg, vb, vy, vpat; 12 __vector float vfr, vfg, vfb, vfy; 13 14 __vector float vrconst = (__vector float) { 0.29891f, 0.29891f, 0.29891f, 0.29891f }; 15 __vector float vgconst = (__vector float) { 0.58661f, 0.58661f, 0.58661f, 0.58661f }; 16 __vector float vbconst = (__vector float) { 0.11448f, 0.11448f, 0.11448f, 0.11448f }; 17 __vector float vfzero = (__vector float) { 0.0f, 0.0f, 0.0f, 0.0f }; 18 __vector unsigned int vmax = (__vector unsigned int) { 255, 255, 255, 255 }; 19 20 __vector unsigned char vpatr = (__vector unsigned char) { 0x10, 0x10, 0x10, 0x00, 21 0x10, 0x10, 0x10, 0x04, 22 0x10, 0x10, 0x10, 0x08, 23 0x10, 0x10, 0x10, 0x0c }; 24 __vector unsigned char vpatg = (__vector unsigned char) { 0x10, 0x10, 0x10, 0x01, 25 0x10, 0x10, 0x10, 0x05, 26 0x10, 0x10, 0x10, 0x09, 27 0x10, 0x10, 0x10, 0x0d }; 28 __vector unsigned char vpatb = (__vector unsigned char) { 0x10, 0x10, 0x10, 0x02, 29 0x10, 0x10, 0x10, 0x06, 30 0x10, 0x10, 0x10, 0x0a, 31 0x10, 0x10, 0x10, 0x0e }; 32 __vector unsigned char vpaty = (__vector unsigned char) { 0x03, 0x03, 0x03, 0x10, 33 0x07, 0x07, 0x07, 0x10, 34 0x0b, 0x0b, 0x0b, 0x10, 35 0x0f, 0x0f, 0x0f, 0x10 }; 36 __vector unsigned char vzero = (__vector unsigned char) { 0, 0, 0, 0, 0, 0, 0, 0, 37 0, 0, 0, 0, 0, 0, 0, 0 }; 38 39 for (i = 0; i < num/4; i++) { 40 vr = (__vector unsigned int) vec_perm(vsrc[i], vzero, vpatr); 41 vg = (__vector unsigned int) vec_perm(vsrc[i], vzero, vpatg); 42 vb = (__vector unsigned int) vec_perm(vsrc[i], vzero, vpatb); 43 44 vfr = vec_ctf(vr, 0); 45 vfg = vec_ctf(vg, 0); 46 vfb = vec_ctf(vb, 0); 47 48 vfy = vec_madd(vfr, vrconst, vfzero); 49 vfy = vec_madd(vfg, vgconst, vfy); 50 vfy = vec_madd(vfb, vbconst, vfy); 51 52 vy = vec_ctu(vfy, 0); 53 54 vpat = vec_cmpgt(vy, vmax); 55 vy = vec_sel(vy, vmax, vpat); 56 57 vdst[i] = (__vector unsigned char) vec_perm(vy, (__vector unsigned int) vzero, vpaty); 58 } 59 60 return; 61 }
|
|
【Program Description】
Calculation of brightness Y is performed in nearly the same way as the floating-point calculation explained for Practice Program (2-2). Conversion from __vector unsigned char to __vector float data is performed in two steps: first, from __vector unsigned char to __vector unsigned int, and then to __vector float.
For the first part of the conversion, the vec_perm() function is used. The second part of the conversion is enabled by the use of the vec_ctf() function. Thereafter, the vec_madd() function iterates calculations based on the multiplication formula explained in the question part of this section.
Upon completion of multiplications, the vec_ctu() function converts floating-point numbers into integer values. We only touched upon this function in Table 2.4, but we hope you still remember it.
Last of all, each calculated result is rounded off at the maximum value of 255 by employing the method to eliminate conditional branches explained for Practice Program (2-3).
Fig. 2.27: Grayscale Conversion Processing by SIMD Operations
The source code used in the above solution program is as follows.
Lines 5〜6 Used to enable scalar to vector pointer cast, making it possible to refer to scalar arrays src and dst in an equivalent vector form. Lines 8〜9 Vector variables used to store RGB data for SIMD operations. Lines 11〜15 Vector constants for calculating brightness Y. Lines 17〜28 Realignment patterns necessary to generate vectors realigned into R, G and B element groups. Lines 29〜34 Realignment patterns used to realign brightness data Y in conformity with the output data format. Lines 37〜39 Used to convert input data into vectors grouped in RGB units. Lines 41〜43 Using the vec_ctf() function, convert RGB data into floating-point values. Lines 45〜47 Used to calculate brightness Y. Line 49 Using the vec_ctu() function, convert brightness data Y into integer values. Lines 51〜52 Using vec_cmpgt() and vec_sel() functions, round off each calculated result so that it falls in the range of values that can be expressed by an 8-bit unsigned integer. Lines 54 Used to send and store grayscale data in the output buffer dst.
|
2.10 Chapter Summary
In summary, this chapter has covered the following five aspects of SIMD operations.
(1) SIMD Operation Overview
(2) Data Used in SIMD Programming
(3) Rudimentary SIMD Operations
(4) Generation of SIMD-Ready Vectors
(5) Elimination of Conditional Branches
Major Points of Discussion in Section 2.1: SIMD Operation Overview
The basic principle of SIMD operations lies, as stated repeatedly, in processing multiple data with a single instruction. Despite this advantage, however, SIMD operations can only be applied to certain predefined processing patterns.
Major Points of Discussion in Section 2.2: Data Used in SIMD Programming
With the Cell, SIMD operations use 128-bit (16-byte) fixed-length vectors made up of 2 to 16 elements according to the data type. SIMD operations can utilize both scalars and vectors by performing a pointer cast between the two types of data.
Major Points of Discussion in Section 2.3: Rudimentary SIMD Operations
SIMD operations make use of the built-in functions of the VMX instruction set to perform arithmetic operations.
Major points of Discussion in Section 2.4: Generation of SIMD-Ready Vectors
The data structure of the inputs to application programs are not always suited for SIMD operations. This section has therefore been provided to explain how to convert such inputs into vectors convenient for SIMD operations.
Major Points of Discussion in Section 2.5: Elimination of Conditional Branches
Efficiency of SIMD operations is significantly affected if conditional branches were to be used in the same way as in scalar operations. SIMD operations therefore employ a second method to obtain the same result as conditional branching.
Basics of SIMD operations have been explained in this chapter. We hope that the information presented, as well as the practice programs you have worked on, was useful and helpful. Now then, let’s proceed to the next chapter on developing programs for SPE processors.